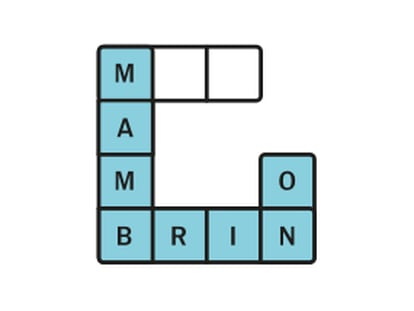
Una de cada cinco
Resolvemos el 30º desafío matemático de EL PAÍS con el que celebramos el centenario de la Real Sociedad Matemática Española.- La ganadora de es M.ª Belén Ramos Álvarez, de Valladolid.
Ya hay solución para el trigésimo desafío matemático con el que EL PAÍS celebra el centenario de la Real Sociedad Matemática Española (ver el vídeo conmemorativo).
Santiago Fernández Fernández, asesor de matemáticas del Berritzegune Nagusia de Bilbao y responsable de la sección de retos matemáticos del portal Divulgamat, propuso el problema (ver vídeo de la izquierda) y lo resuelve ahora (vídeo de la derecha).
Para este desafío se han recibido en el plazo marcado 660 respuestas, de las que el 88% eran correctas. La ganadora de una biblioteca matemática como la que entrega cada semana EL PAÍS ha sido en esta ocasión M.ª Belén Ramos Álvarez, de Valladolid.
Recordemos el problema: una persona necesita urgentemente 5.000 euros y los puede conseguir jugando a un juego de azar que consiste en apostar una cantidad de dinero, que ha de ser siempre múltiplo de 1.000, de tal manera que, si gana, recupera lo apostado y consigue además otro tanto.
El jugador parte con 1.000 euros y juega siempre en cada apuesta de la manera más arriesgada posible para lograr su objetivo, dentro de la lógica (por ejemplo: si tiene 2.000 euros se jugará los 2.000, mientras que si hubiera conseguido 3.000 euros no los jugaría en su totalidad, sino que apostaría únicamente 2.000 euros, ya que en el caso de ganar conseguiría los 5.000 euros y si perdiera se quedaría con 1.000, con la posibilidad de volver a jugar).
Nota importante: Se supone que en cada lance la probabilidad de perder o de ganar es la misma.
La pregunta es: ¿Qué probabilidad tiene de conseguir los 5.000 euros?
Respuesta: 1/5
La primera de las dos soluciones que se presentan en el vídeo, consistente en realizar una simulación, coincide con la que propone Rafael Losada. La segunda solución, del profesor Fernández, por la que han optado la mayoría de los concursantes, recurre al estudio de un árbol de probabilidad, como lo hace Ángel T. Jorge González, para posteriormente calcular la probabilidad mediante la suma de una serie infinita P = (1/2^3 + 1/2^4) + (1/2^7 + 1/2^8) + (1/2^11 + 1/2^12) + (1/2^15 + 1/2^16) + ....... = 1/5.
Muchos de los que enviaron soluciones correctas han utilizado un razonamiento del siguiente tipo (transcribimos el de Antonio González Lahoz):
P1=posibilidad de ganar 5.000 teniendo 1.000 (lo que se pide)
P2= posibilidad de ganar 5.000 teniendo 2.000
P3=posibilidad de ganar 5.000 teniendo 3.000
P4= posibilidad de ganar 5.000 teniendo 4.000
-Cuando tenemos 1.000 apostamos 1.000 y existe 1/2 de posibilidades de obtener 2.000 y otro medio de perder, luego: P1=1/2*P2.
-Cuando tenemos 2.000 apostamos 2.000 y existe 1/2 de posibilidades de obtener 4.000 y otro medio de perder, luego: P2=1/2*P4.
-Cuando tenemos 3.000 apostamos 2000 y existe 1/2 de posibilidades de obtener 5.000 (ganar) y otro medio de quedarnos en 1.000, luego: P3=1/2+1/2*P1.
-Cuando tenemos 4.000 apostamos 1.000 y existe 1/2 de posibilidades de obtener 5.000 (ganar) y otro medio de quedarnos en 3.000, luego: P4=1/2+1/2*P3.
Con esto se tiene un sistema de cuatro ecuaciones y cuatro incógnitas, cuya solución es: P1=1/5, P2=2/5, P3=3/5, P4=4/5
También ha habido un grupo nutrido de participantes que ha resuelto el desafío acudiendo al concepto de esperanza matemática, como muy bien explica Ángel Pastor Martín. De acuerdo a su presentación, la justificación es la siguiente:
Estamos ante un juego equilibrado o justo, por lo tanto la esperanza de dinero ganado es 0 euros. Además, las dos únicas formas de terminar el juego son con 0 o con 5.000 euros, lo que supone ganar -1-000 euros o 4.000 euros, respectivamente.
Llamamos p a la probabilidad de alcanzar los 5.000 euros (ganando 4.000), con lo que 1-p es la probabilidad de quedarse sin los 1000 euros que tenía inicialmente. La esperanza del dinero ganado, E, tiene que ser cero, y la expresión E = 4.000p-1.000(1-p)=0 nos lleva al resultado. Resolviendo la ecuación se obtiene 4.000p-1.000+1.000p=0, luego 5.000p=1.000, luego p=0,2.
Un buen número de concursantes ha recurrido a un razonamiento similar al siguiente. Partimos con 1.000 euros y ahora probabilidad 1/2 de perder y quedarse con 0 euros, y la misma de ganar y quedarse con 2.000. En el segundo caso apostamos 2.000 y la probabilidad de perder es 1/4 para quedarse con 0, y la misma para ganar y obtener 4.000. Seguimos apostando 1.000 con probabilidad 1/8 de ganar y quedarse con 5.000 euros y la misma probabilidad de perder y quedarse con 3.000 euros. Ahora apostamos 2.000, siendo 1/16 la probabilidad de ganar y quedarse con 5.000, y la misma probabilidad de perder y quedarse con 1.000.
Como se puede ver, esta es la situación de partida, por lo que ahora se va a repetir el proceso. Por tanto, llamando P a la probabilidad buscada tenemos que se cumple la ecuación P=1/8+1/16+(1/16)P, que al resolverla da la solución P =1/5, o bien un 20%.
Por último, son de reseñar algunas soluciones en las que se emplean conocimientos estocásticos, señalando que se trata de una cadena de Markov con seis estados (dos de ellos absorbentes) para acabar resolviendo el sistema de cuatro ecuaciones y cuatro incógnitas asociado a dicha cadena. Algunos lectores también han utilizado asistentes matemáticos para realizar simulaciones y poder hacer las sumas pertinentes.
En todo caso, hay que señalar que el jugador se enfrenta al desafío de la apuesta con una vida infinita, aspecto reseñable para poder resolver el problema en toda su extensión.
El jueves plantearemos un nuevo reto. Y recordamos a los lectores que pueden enviar los suyos.