El desafío de Dido de Tiro
EL PAÍS y la RSME presentan el segundo desafío matemático del verano Entre los acertantes se sorteará una colección de libros 'Grandes Ideas de la Ciencia'
EL PAÍS y la Real Sociedad Matemática Española plantean el segundo desafío matemático del verano. En esta ocasión, presenta el desafío la doctora Mari Luz García Escamilla, gestora del Posgrado en Matemáticas de la Universidad Autónoma de Madrid.
Entre los acertantes se sorteará una colección de libros Grandes Ideas de la Ciencia. Las soluciones deberán enviarse al correo electrónico desafiodeagosto2@gmail.com antes de las 00.00 del martes 12 de agosto (medianoche del lunes al martes).
Para evitar errores y en atención a nuestros lectores sordos, además del vídeo donde se plantea el desafío, publicamos a continuación el enunciado por escrito:
El poeta latino Virgilio cuenta en la Eneida como la princesa Dido de Tiro llegó a la costa del norte de África huyendo de su hermano el rey Pigmalión. Al llegar le pidió a Jarbas, rey de los gétulos, un terreno donde asentarse. Jarbas le contestó dándole una piel de buey y comprometiéndose a regalarle toda la tierra que pudiera abarcar con ella.
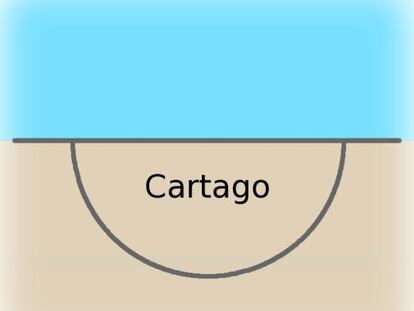
Lo primero que hizo Dido fue mandar cortar la piel en una tira muy fina. Después pensó que abarcaría más terreno si utilizaba, además de la cuerda fabricada con la piel de buey, la costa. Así, colocando los extremos de la cuerda en la playa abarcó el terreno donde fundó después la ciudad de Cartago.
Nosotros vamos a presentar este mismo problema pero algo simplificado, ya que vamos a considerar que la costa que utilizó Dido era una línea recta. Con esta condición, la forma en la que hay que colocar la cuerda para abarcar la mayor superficie posible es una semicircunferencia con los extremos en la costa. Esta solución, que se muestra en la figura de abajo a modo de ejemplo, la vamos a suponer conocida.
Y ahora, nuestro reto. El desafío que proponemos esta semana consiste en calcular el área de la superficie más grande que Dido puede abarcar con las siguientes condiciones:
1. La costa donde se va a establecer es un cabo formado por un ángulo de 45 grados y dos lados rectos, como en esta figura:
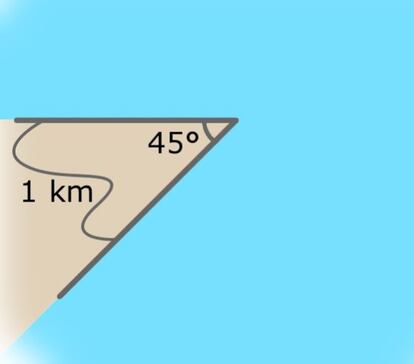
2. Dido ha conseguido sacar una cuerda de 1 kilómetro de longitud de la piel del buey.
Lo que pedimos es el valor del área de la superficie máxima que se puede formar con estas condiciones y una explicación de por qué no se puede hacer mejor.
ADVERTENCIA: No se considerarán válidas las respuestas en las que se utilicen derivadas, cálculo de variaciones, ni herramientas similares. Sí se puede usar, sin necesidad de justificar, la respuesta al problema simplificado comentada anteriormente como ejemplo.